Set I - Delhi
SECTION A
Q. 8. What is the angle subtended at the centreof a circle of radius 7 cm, by an arc of length 11 cm?
Ans . 90°
Sol .
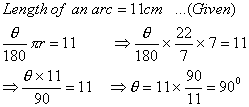
Q. 10 . A card is drawn at random from a wellshuffled deck of 52 cards. What is the probability of getting a black king?
Ans. 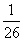
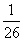
Sol .
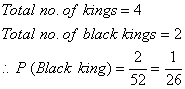
SECTION B
Questions number 11 to 15 carry 2 marks each.
Q. 11. On dividing x3 – 3x2 + x + 2 by a polynomial g(x), the quotient and remainder were x – 2 and – 2x + 4, respectively. Find g(x).
Sol . Dividend = Divisor X Quotient + Remainder
Q. 12. If tan (2A) = cot(A – 21°), where 2A is an acute angle, then find the value of A.
Sol .
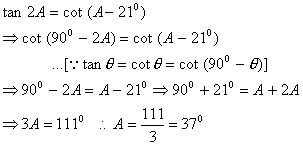
Q. 13. If A(–2, 4), B(0, 0) and C(4, 2) are the vertices of a Δ ABC, then find the length of median through the vertexA.
Ans. 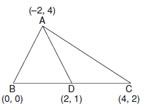

Sol .
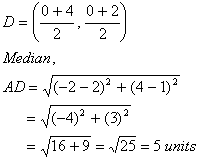
Q. 14. In two concentric circles, a chord of the larger circle touches the smaller circle. If the length of this chord is 8 cm and the diameter of the smaller circle is 6 cm, then find the diameter of the larger circle.
Sol . 

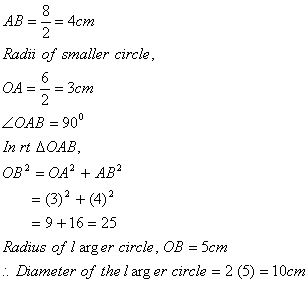
Or
In Fig. 3, PA and PB are two tangents drawn to a circle with centre O, from an external point P such that PA = 5 cm and 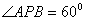 . Find the length of chord AB.
. Find the length of chord AB.
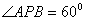 . Find the length of chord AB.
. Find the length of chord AB.Sol .
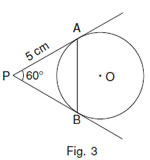
PA = PB


Q. 15. Find the probability that a number selected at random from the numbers 3, 4, 5,…, 25 is prime.
Sol . Total given numbers = 23 Prime numbers are 3, 5, 7, 11, 13, 17, 19, 23 = 8
Prob. (Prime number) =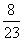
Prob. (Prime number) =
SECTION C
Questions number 16 to 25 carry 3 marks each.
Q. 16. Prove that 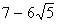 is an irrational number.
is an irrational number.
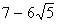 is an irrational number.
is an irrational number.Sol.
Let us assume, to the contrary, that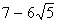 is rational That is, we can find coprimes a and b
is rational That is, we can find coprimes a and b 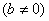 such that
such that
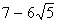 is rational That is, we can find coprimes a and b
is rational That is, we can find coprimes a and b 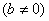 such that
such that 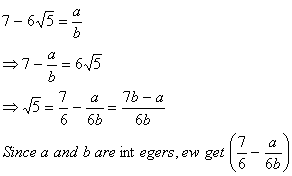
is rational, and so
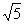 is rational But this contradicts the fact that
is rational But this contradicts the fact that 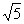 is irrational. This contradiction has arisen because of our incorrect assumption that
is irrational. This contradiction has arisen because of our incorrect assumption that 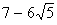 is rational. So, we conclude that
is rational. So, we conclude that 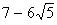 is irrational.
is irrational.Q. 17. Check graphically whether the pair of equations 3x + 5y = 15 and x – y = 5 is consistent. Also find the coordinates of the points where the graphs of the equations meet the y-axis.
Sol .
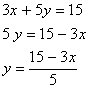
| x | 0 | -5 | 5 |
| y | 3 | 6 | 0 |
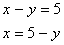
| x | 5 | 7 | 3 |
| y | 0 | 2 | -2 |
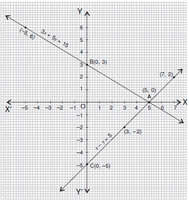
By plotting the points and joining them, the lines intersect at A(5, 0)
 x = 5, y = 0
x = 5, y = 0
 The pair of given equation is consistent.
The pair of given equation is consistent.
The equation 3x + 5y = 15 meets the y-axis at
B(0, 3)The equation x – y = 5 meets the y-axis at C(0, – 5)
The equation 3x + 5y = 15 meets the y-axis at
B(0, 3)The equation x – y = 5 meets the y-axis at C(0, – 5)
Or
Places A and B are 160 km apart on a highway. One car starts from A and another from B at the same time. If the cars travel in the same direction at different speeds, they meet in 8 hours, but if they travel towards each other, they meet in 2 hours. What are the speeds of the two cars?
Sol .
Let the speed of 1st car starting from place A = x km/hr
and the speed of 2nd car starting from place B = y km/hr
When two cars travel in the same direction
Distance covered by 1st car in 8 hours
= 160 km + Distance covered by 2nd car
8x = 8y + 160 …( Q Distance = Speed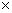 time)
time)
x = y + 20 …(i) (Dividing both sides by 8)
When two cars travel towards each other
2x + 2y = 160 …( D = S
D = S 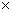 T)
T)
x + y = 80 …(Dividing both sides by 2)
y + 20 + y = 80 …[From (i)]
2y = 80 – 20 = 60
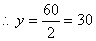
From (i), x = 30 + 20 = 50
 Speed of car starting from place A = 50 km/hr
Speed of car starting from place A = 50 km/hr
and speed of car starting from place B = 30 km/hr.
and the speed of 2nd car starting from place B = y km/hr
When two cars travel in the same direction
Distance covered by 1st car in 8 hours
= 160 km + Distance covered by 2nd car
8x = 8y + 160 …( Q Distance = Speed
x = y + 20 …(i) (Dividing both sides by 8)
When two cars travel towards each other
2x + 2y = 160 …(
x + y = 80 …(Dividing both sides by 2)
y + 20 + y = 80 …[From (i)]
2y = 80 – 20 = 60
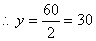
From (i), x = 30 + 20 = 50
and speed of car starting from place B = 30 km/hr.
Q. 18. Find the roots of the equation :
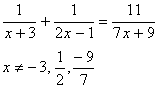
Sol .
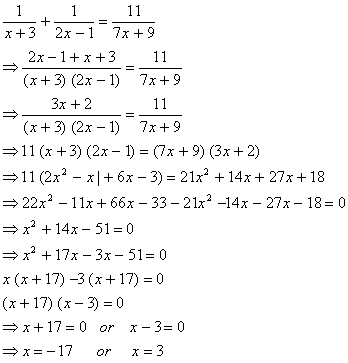
Q. 19. Find the sum of all three digit numbers which are divisible by 7.
Sol. To find : 105 + 112 + 119 + … + 994
Ist term, a = 105
Common difference, d = 112 – 105 = 7
an = 994
a + (n – 1)d = 994
105 + (n – 1)7 = 994
(n – 1)7 = 994 – 105 = 889
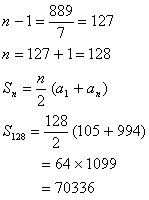
Ist term, a = 105
Common difference, d = 112 – 105 = 7
an = 994
a + (n – 1)d = 994
105 + (n – 1)7 = 994
(n – 1)7 = 994 – 105 = 889
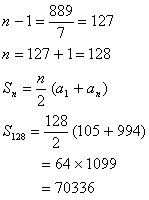
Q. 20. Prove that :
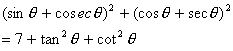
Sol. See Q. 20, 2008(I OD).
Or
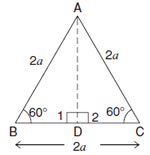
Using Geometry, find the value of sin 60°.
Sol.
Δ ABC be an equilateral, Let each side be 2a. Since each angle in equilateral Δ is 60°

Q. 21. Show that the points (1, 1), (–1, 5), (7, 9) and (9, 5) taken in that order, are the vertices of a rectangle.
Sol. Let A(1, 1), B(– 1, 5), C(7, 9) and D(9, 5) Using Distance formula
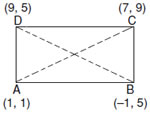
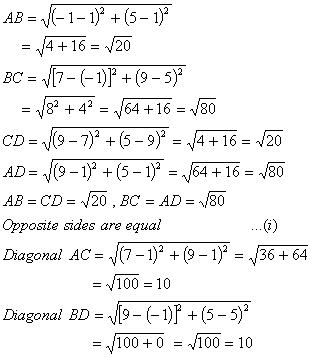
Diagonal AC = Daigonal BD = 10
∴ Diagonals are equal …(ii)
From (i) and (ii), we get
Points A, B, C and D are the vertices of a rectangle.
∴ Diagonals are equal …(ii)
From (i) and (ii), we get
Points A, B, C and D are the vertices of a rectangle.
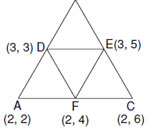
Q. 22. Find the area of the triangle formed by joining the mid-points of the sides of the trianglewhose vertices are (2, 2), (4, 4) and (2, 6).
Sol. Let A(2, 2), B(4, 4), C(2, 6)
Mid-point of AB,
Mid-point of AB,
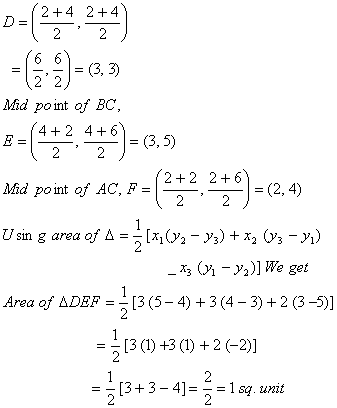
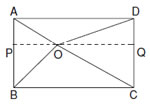
Q. 23. In Fig. 4, O is any point inside a rectangle ABCD such that OB = 6 cm, OD = 8cm and OA = 5 cm.Find the length of OC.
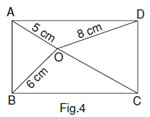
Sol. Through O, draw
PQ || BC
So that P lies on AB
and Q lies on DC.
PQ || BC
PQ || BC
So that P lies on AB
and Q lies on DC.
PQ || BC


Q. 24. Draw a line segment AB of length 7 cm.Taking A as centre, draw a circle of radius 3 cm and taking B as centre, draw another circle ofradius 2.5 cm. Construct tangents to each circle from the centre of the other circle.
Sol : 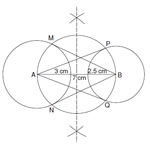

PA and QA are the two tangents drawn from centre A MB and NB are the two tangents drawn from centre B.
Q. 25. A round table cover has six equal designs as shown in Fig. 5. If the radius of the cover is 35 cm, then find the total area of the designs.
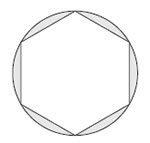

Sol :
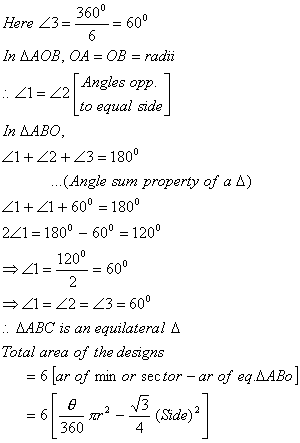
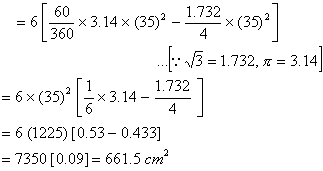
Or
In Fig. 6, ABC is a right angled triangle with B = 90°, AB = 48 cm andBC = 14 cm. With AC as diameter a semicircle is drawn and with BC asradius a quadrant of a circle is drawn. Find the area of the shaded region.
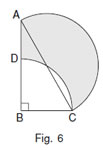
Sol .

SECTION D
Questions number 26 to 30 carry 6 marks each.
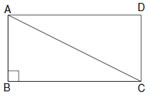
Q. 26. The diagonal of a rectangular field is 60 metres more than the shorter side. If the longer side is 30 metres more than the shorter side, find the sides of the field.
Sol. Let shorter side, AB = x m then Diagonal, AC = (x + 60) m and longer side,
BC = (x + 30) m In rt. Δ ABC,
BC = (x + 30) m In rt. Δ ABC,

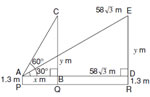
Q. 27. A boy, who’s eye level is 1.3 m from the ground, spots a balloon moving with the wind in a horizontal line at some height from the ground. The angle of elevation of the balloon from the eyes of the boy at any instant is 60°. After 2 seconds, the angle of elevation reduces to 30°. If the speed of wind at that moment is 29 3 m/s, then find the height of the balloon from the ground.
Sol. Let AP be the boy, C and E are two positions
of the balloon. Speed of wind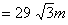
Distance travelled by the balloon in 2 seconds,
CE = BD =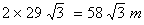
Let AB = x m and BC = DE = y m
of the balloon. Speed of wind
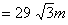
Distance travelled by the balloon in 2 seconds,
CE = BD =
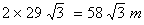
Let AB = x m and BC = DE = y m
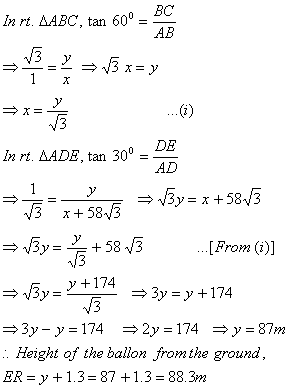
Or
A statue, 1.5 m tall, stands on the top of a pedestal. From a point on the ground, the angle of elevation of the top of the statue is 45° and from the same point the angle of elevation of the top of the pedestal is 30°. Find the height of the pedestal. 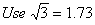
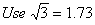
Sol. Let BC = h m
be the pedestal.
CD be the statue.
Distance from the
point be AB = x m
In rt.,
be the pedestal.
CD be the statue.
Distance from the
point be AB = x m
In rt.,
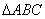
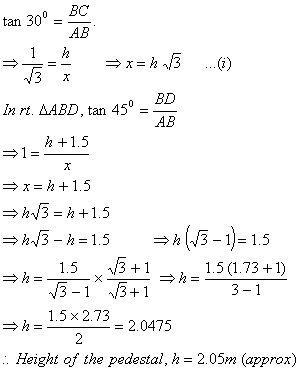
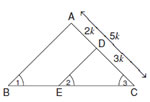
Q. 28 . Prove that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides. Using the above, do the following .
If D is a point on the side AC of 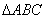 such that
such that
AD : DC = 2 : 3, and E is a point on BC such that
DE || AB; then find the ratio of areas of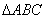 and
and 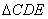 .
.
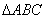 such that
such thatAD : DC = 2 : 3, and E is a point on BC such that
DE || AB; then find the ratio of areas of
 and
and  .
.Sol. Part I: See Theorem 2,
Page (xxxi).
Part II:
Let AD = 2k, CD = 3k
Then AC = 2k + 3k = 5k
Page (xxxi).
Part II:
Let AD = 2k, CD = 3k
Then AC = 2k + 3k = 5k

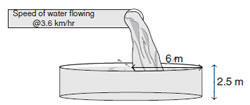
Q. 29. A farmer connects a pipe of internal diameter 25 cm from a canal into a cylindrical tank in his field, which is 12 m in diameter and 2.5 m deep. If water flows through the pipe at the rate of 3.6 km/h, in how much time will the tank be filled? Also find the cost of water, if the canal department charges at the rate of Rs. 0.07/m3.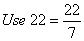
Sol.

Or
A spherical glass vessel has a cylindrical neck 7 cm long and 4 cm in diameter. The diameter of the spherical part is 21 cm. Find the quantity of water. it can hold .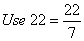
Sol .
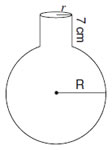
Height of cylindrical neck , h = 7 cm
Radius of cylindrical neck,
Radius of cylindrical neck,

Q. 30. The distribution below gives the weights of 30 students of a class. Find the mean and the median weight of the students.
| Weight(in Kg) | Number of Student |
| 40 - 45 | 2 |
| 45 - 50 | 3 |
| 50 -55 | 8 |
| 55 - 60 | 6 |
| 60 - 65 | 6 |
| 65 -70 | 3 |
| 70 - 75 | 2 |
Sol .
| Weight(in Kg) fi | Number of Student | xi |  | 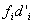 | c.f. | |
| 40-45 | 2 | 42.5 | -3 | -6 -6 -8 | -20 | 2 |
| 45-50 | 3 | 47.5 | -2 | 5 | ||
| 50-55 | 8 | 52.5 | -1 | 13 | ||
| 55-60 | 6 | 57.5 | 0 | 0 | 19 | |
| 60 -65 | 6 | 62.5 | 1 | 6 6 6 | -18 | 25 |
| 65 - 70 | 3 | 67.5 | 2 | 28 | ||
| 70 -75 | 2 | 72.5 | 3 | 30 | ||
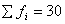 | 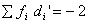 | |||||
No comments:
Post a Comment