MATHEMATICS
Set I - Outside Delhi
Q. 9. Write the lower limit of the median class in the following frequency distribution .
| Classes. | 0–10 | 10–20 | 20–30 | 30–40 | 40–50 |
| Frequency. | 9 | 12 | 5 | 16 | 8 |
Ans. 20
Sol .
| Class | F | c.f |
| 0 - 10 | 8 | 9 |
| 10 - 20 | 12 | 12 |
| 20 - 30 | 5 | 26 |
| 30- 40 | 16 | 42 |
| 40- 50 | 8 | 50 |
Q. 10. Cards each marked with one of the numbers 6, 7, 8, …, 15 are placed in a box and mixed thoroughly. One card is drawn at random from the box. What is the probability of getting a card with number less than 10?
Ans .
Sol. Total no. of cards = 10
Number of cards less than 10 = 6, 7, 8, 9 i.e. 4
Reqd. probability =
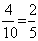
SECTION B
Questions number 11 to 15 carry 2 marks each.
Q. 11. What real number should be subtracted from the polynomial 3x3 + 10x2 – 14x + 9 so that the polynomial 3x – 2 divides it exactly?
Sol.
5 should be subtracted from 3x3 + 10x2– 14x + 9 So that the polynomial (3x – 2) divides it exactly
Q. 12. Evaluate .
Sol.
Q. 13. Find a relation between x and y if the points (2, 1), (x, y) and (7, 5) are collinear.
Sol . Let A(2, 1), B(x, y) and C(7, 5) Pts. A, B, C are collinear … (Given)
 2(y – 5) + x(5 – 1) + 7(1 – y) = 0
2(y – 5) + x(5 – 1) + 7(1 – y) = 0
 2y – 10 + 5x – 5 + 7 – 7y = 0
2y – 10 + 5x – 5 + 7 – 7y = 0
 5x – 5y – 8 = 0
5x – 5y – 8 = 0
or
5x – 5y = 8
 2(y – 5) + x(5 – 1) + 7(1 – y) = 0
2(y – 5) + x(5 – 1) + 7(1 – y) = 0 2y – 10 + 5x – 5 + 7 – 7y = 0
2y – 10 + 5x – 5 + 7 – 7y = 0 5x – 5y – 8 = 0
5x – 5y – 8 = 0 or
5x – 5y = 8
Q. 14. ABC is a right triangle, right angled at A, and D is the mid-point of AB. Prove that
BC2 = CD2 + 3BD2
BC2 = CD2 + 3BD2
Sol.
Inrt
BC2 = CA2 + AB2.
…(Pythagoras’ theorem)
BC2 = (CD2 – AD2) + (2AD)2
∆ BAC,
BC2 = CA2 + AB2.
…(Pythagoras’ theorem)
BC2 = (CD2 – AD2) + (2AD)2
BC2 = CD2 – AD2 + 4AD2
= CD2 + 3AD2
 BC2 = CD2 + 3BD2
BC2 = CD2 + 3BD2…….
Q. 15. Two dice are thrown at the same time. Find the probability that the sum of the two numbers appearing on the top of the dice is more than 9.
Sol. Two dice can be thrown as 6 X 6 = 36 ways
“a total more than 9” can be obtained as
(4, 6), (6, 4), (5, 5), (5, 6), (6, 5), (6, 6) i.e. 6 ways
Required Probability =
“a total more than 9” can be obtained as
(4, 6), (6, 4), (5, 5), (5, 6), (6, 5), (6, 6) i.e. 6 ways
Required Probability =
Or
A game consists of tossing a one-rupee coin 3 times and noting its outcome each time. Hanif wins if all the tosses give the same result i.e. three heads or three tails, and loses otherwise. Calculate the probability that Hanif will lose the game.
Sol. S = {HHH, HHT, HTH, THH, TTH, THT, HTT, TTT}
P (Hanif wins) = P (three heads or three tails)
=
P (Hanif loses) = 1 – P(Hanif wins)
P (Hanif wins) = P (three heads or three tails)
=
P (Hanif loses) = 1 – P(Hanif wins)
SECTION C
Q. 18. Check graphically whether the pair of equations 3x – 2y + 2 = 0 and 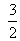 x – y + 3 = 0, is consistent. Also find the coordinates of the points where the graphs of the equations meet the y-axis.
x – y + 3 = 0, is consistent. Also find the coordinates of the points where the graphs of the equations meet the y-axis.
3x – 2y + 2 = 0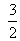 x – y + 3 = 0
x – y + 3 = 0
 3x + 2 = 2y
3x + 2 = 2y 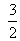 x + 3 = y
x + 3 = y

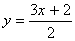
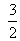 x – y + 3 = 0, is consistent. Also find the coordinates of the points where the graphs of the equations meet the y-axis.
x – y + 3 = 0, is consistent. Also find the coordinates of the points where the graphs of the equations meet the y-axis.3x – 2y + 2 = 0
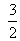 x – y + 3 = 0
x – y + 3 = 0 3x + 2 = 2y
3x + 2 = 2y 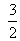 x + 3 = y
x + 3 = y
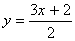
Sol. 3x – 2y + 2 = 0 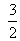 x – y + 3 = 0
x – y + 3 = 0
 3x + 2 = 2y
3x + 2 = 2y 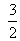 x + 3 = y
x + 3 = y

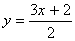
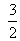 x – y + 3 = 0
x – y + 3 = 0 3x + 2 = 2y
3x + 2 = 2y 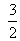 x + 3 = y
x + 3 = y
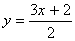
| x | 0 | 2 | -2 |
| y | 1 | 4 | -2 |
| x | 0 | 2 | -2 |
| y | 3 | 6 | 0 |
By plotting the points and joining them, the lines donot intersect anywhere, i.e., they are parallel.
 Given pair of equations is not consistent, i.e., inconsistent.
Given pair of equations is not consistent, i.e., inconsistent. The equation 3x – 2y + 2 = 0 meets the y-axis at A(0, 1)
The equation 3x – 2y + 2 = 0 meets the y-axis at A(0, 1) The equation
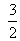 x – y + 3 = 0 meets the y-axis at B(0, 3).
x – y + 3 = 0 meets the y-axis at B(0, 3).Or
A fraction becomes 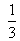 , if 2 is added to both numerator and denominator. If 3 is added to both numerator and denominator, it becomes
, if 2 is added to both numerator and denominator. If 3 is added to both numerator and denominator, it becomes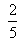 . Find the fraction.
. Find the fraction.Sol. Let the fraction by
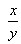
According to the question
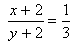
3x + 6 = y + 2
3x – y = 2 – 6
3x – y = –4
3x + 4 = y …(i)
3x – y = 2 – 6
3x – y = –4
3x + 4 = y …(i)
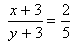
5x + 15 = 2y + 6
5x – 2y = 6 – 15
5x – 2y = – 9
5x – 2(3x + 4) = – 9
…[From (i)
5x – 6x – 8 = – 9
– x = – 9 + 8
– x = – 1
x = 1
From (i), y = 3(1) + 4 = 7
 The fraction x/y =4/7
The fraction x/y =4/7
Q. 19. Find the middle term of the A.P. 10, 7, 4, …, (– 62) .5x – 2y = 6 – 15
5x – 2y = – 9
5x – 2(3x + 4) = – 9
…[From (i)
5x – 6x – 8 = – 9
– x = – 9 + 8
– x = – 1
x = 1
From (i), y = 3(1) + 4 = 7
 The fraction x/y =4/7
The fraction x/y =4/7Sol. 1 st term, a = 10
Common difference, d = 7 – 10 = – 3
an = – 62
 a + (n – 1)d = – 62
a + (n – 1)d = – 62 10 + (n – 1) (– 3) = – 62
10 + (n – 1) (– 3) = – 62 (n – 1) (– 3) = – 62 – 10 = – 72
(n – 1) (– 3) = – 62 – 10 = – 72 n – 1 =
n – 1 =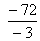 = 24
= 24  n = 24 + 1 = 25
n = 24 + 1 = 25Middle term = 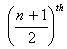 term
term 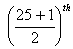 term=13th term
term=13th term
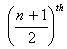 term
term 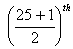 term=13th term
term=13th terman = a + (n – 1)d  a13 = a + 12d
a13 = a + 12d
 a13 = 10 + 12(– 3) = 10 – 36 = – 26
a13 = 10 + 12(– 3) = 10 – 36 = – 26
 a13 = a + 12d
a13 = a + 12d a13 = 10 + 12(– 3) = 10 – 36 = – 26
a13 = 10 + 12(– 3) = 10 – 36 = – 26Q. 20. For an acute angle  show that
show that
 show that
show that(sin  – cosec
– cosec  ) (cos
) (cos  – sec
– sec  ) =
) = 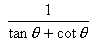
 – cosec
– cosec  ) (cos
) (cos  – sec
– sec  ) =
) = 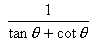
Sol. LHS = (sin  – cosec
– cosec ) (cos
) (cos  – sec
– sec  )
)
=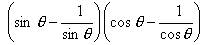
=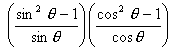
=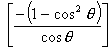
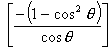
=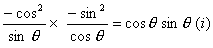
 – cosec
– cosec ) (cos
) (cos  – sec
– sec  )
)=
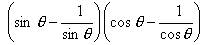
=
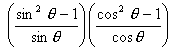
=
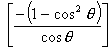
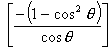
=
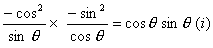
RHS=
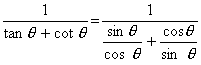
=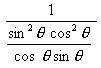
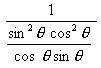
=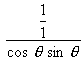 …..[
…..[ cos2
cos2  +sin2
+sin2  = 1]
= 1]
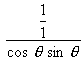 …..[
…..[ cos2
cos2  +sin2
+sin2  = 1]
= 1]= cos  + sin
+ sin  …(ii)
…(ii)
 + sin
+ sin  …(ii)
…(ii)From (i) and (ii) LHS = RHS
Q. 21. Point P, Q, R and S in that order are dividing a line segment joining A(2, 6) and B(7, – 4) in five equal parts. Find the coordinates of P and R.
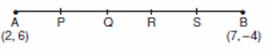
AP : PB = 1 : 4
P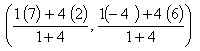
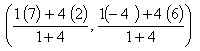
=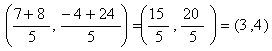
AR:RB=3:2
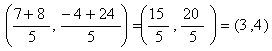
AR:RB=3:2
R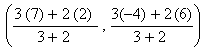
=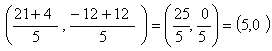
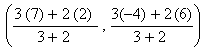
=
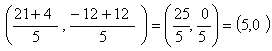
Q. 22. A (– 4, – 2), B(– 3, – 5), C(3, – 2) and D(2, k) are the vertices of a quadrilateral ABCD. Find the value of k, if the area of the quadrilateral is 28 sq. units.
Sol.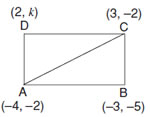

ar( ABC)
ABC)
 ABC)
ABC)= 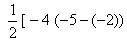 + (-3)[ -2 – (-2 )] + 3[ -2-(-5)] (-4 , -2)
+ (-3)[ -2 – (-2 )] + 3[ -2-(-5)] (-4 , -2)
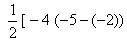 + (-3)[ -2 – (-2 )] + 3[ -2-(-5)] (-4 , -2)
+ (-3)[ -2 – (-2 )] + 3[ -2-(-5)] (-4 , -2)=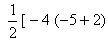 -3 (-2+2 + 3 (-2 + 5) ]
-3 (-2+2 + 3 (-2 + 5) ]
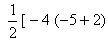 -3 (-2+2 + 3 (-2 + 5) ]
-3 (-2+2 + 3 (-2 + 5) ]=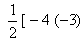 -3(0) + 3 (3 ) ]
-3(0) + 3 (3 ) ]
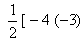 -3(0) + 3 (3 ) ]
-3(0) + 3 (3 ) ]=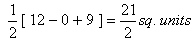
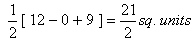
ar ( ABC)ar(
ABC)ar( ABD) =28
ABD) =28
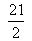 + ar (
+ ar ( ACD)= 28
ACD)= 28
 ABC)ar(
ABC)ar( ABD) =28
ABD) =28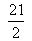 + ar (
+ ar ( ACD)= 28
ACD)= 28 ar ( ACD) =28 -
ACD) =28 - 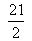 =
= 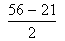 =
=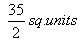

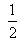 [-4(-2-k) + 3 (k- (-2)) + 2(-2-(-2))] =
[-4(-2-k) + 3 (k- (-2)) + 2(-2-(-2))] = 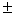
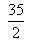
 8 + 4k + 3k + 6 = 35
8 + 4k + 3k + 6 = 35
 7k + 14 = 35
7k + 14 = 35
 k + 2 = 5 …(Dividing both sides by 7)
k + 2 = 5 …(Dividing both sides by 7)
 k =
k = 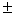 5 – 2
5 – 2
 k = 5 – 2 or k = – 5 – 2
k = 5 – 2 or k = – 5 – 2
 k = 3 or k = – 7
k = 3 or k = – 7
 ACD) =28 -
ACD) =28 - 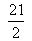 =
= 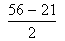 =
=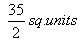
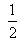 [-4(-2-k) + 3 (k- (-2)) + 2(-2-(-2))] =
[-4(-2-k) + 3 (k- (-2)) + 2(-2-(-2))] = 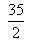
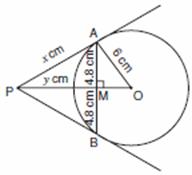
Q. 23. In Fig. 4, AB is a chord of length 9.6 cm, of a circle with centre O and radius 6 cm. The tangents at A and B intersect at P. Find the length of PA.
Then  PAB is an isosceles
PAB is an isosceles  and PO is the angle bisector of
and PO is the angle bisector of 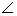 APB
APB
So, OP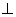 AB and therefore, OP bisects AB which gives
AB and therefore, OP bisects AB which gives
 PAB is an isosceles
PAB is an isosceles  and PO is the angle bisector of
and PO is the angle bisector of 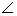 APB
APB So, OP
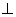 AB and therefore, OP bisects AB which gives
AB and therefore, OP bisects AB which givesAM=MB=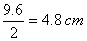
Also OAP=900………….
OAP=900…………. 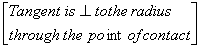
In rt. AMO,OM=
AMO,OM=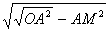
=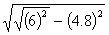
=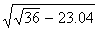
=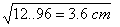
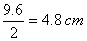
Also
 OAP=900………….
OAP=900…………. 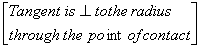
In rt.
 AMO,OM=
AMO,OM=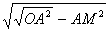
=
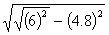
=
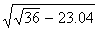
=
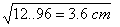
LetPA =xcm and PM = Y cm
In rt AMP, x2 = y2 + (4.8)2 (Pythagoras’ theorem)
AMP, x2 = y2 + (4.8)2 (Pythagoras’ theorem)
X2= y2 + 23.04 …(i)
In rt. ΔPAO, OP2 = PA2 + AO2
…(Pythagoras’ theorem)
(y + 3.6) 2= x2 + (6) 2
In rt
 AMP, x2 = y2 + (4.8)2 (Pythagoras’ theorem)
AMP, x2 = y2 + (4.8)2 (Pythagoras’ theorem)X2= y2 + 23.04 …(i)
In rt. ΔPAO, OP2 = PA2 + AO2
…(Pythagoras’ theorem)
(y + 3.6) 2= x2 + (6) 2
y2 + (3.6) 2 + 2(y) (3.6) = y2 + 23.04 + 36 …[From (i)]
12.96 + 7.2y = 59.04
12.96 + 7.2y = 59.04
7.2y = 59.04 – 12.96 = 46.08
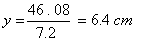
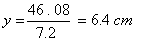
From(i),x2 = y 2+23.04
=(6.4)2+23.04
=40.96+23 .04 = 64
 Tangent, PA ,x =
Tangent, PA ,x =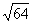 =+8 cm
=+8 cm
=(6.4)2+23.04
=40.96+23 .04 = 64
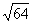 =+8 cm
=+8 cmQ. 24. Construct an isosceles triangle whose base is 9 cm and altitude is 5 cm. Then construct another triangle whose sides are 3/4of the corresponding sides of the first isosceles triangle.
Sol.
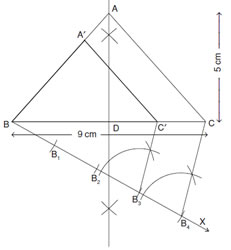
Given
 ABC is an isosceles
ABC is an isosceles  , in which base
, in which baseBC = 9 cm and altitude AD = 5 cm .
 A′BC′is the required
A′BC′is the required  .
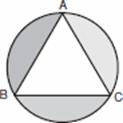
.Q. 25. In a circular table cover of radius 70 cm, a design is formed leaving an equilateral triangle ABC in the middle as shown in Fig. 5. Find the total area of the design.
[ Use 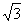 = 1.73,
= 1.73, 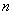 =
= 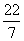 ]
]
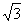 = 1.73,
= 1.73, 
Sol. Join OA, OB and OC. O is the centre.
 ABC is an eq.
ABC is an eq.  .
.
 AOC =
AOC = 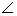 BOC =
BOC = 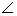 BOA =
BOA =  =
=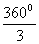 =1200
=1200
Total area of the design = 3(area of segment)
= 3[area of sector – area of ]
]
 ABC is an eq.
ABC is an eq.  .
.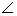 BOC =
BOC =  BOA =
BOA =  =
=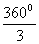 =1200
=1200Total area of the design = 3(area of segment)
= 3[area of sector – area of
 ]
]=3 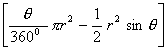
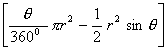
=3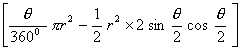
……..( sin2 =2 sin
=2 sin  cos
cos  )
)
=3 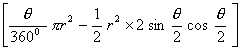
……..( sin2
 =2 sin
=2 sin  cos
cos  )
)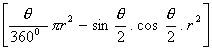
=3 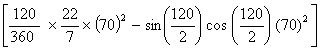
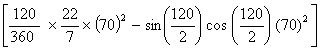
=3x(70)2 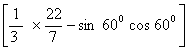
=3x 4900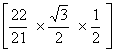
= 14700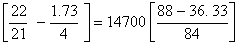
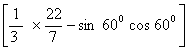
=3x 4900
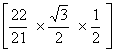
= 14700
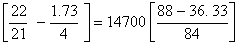
=175 x 51.67 = 9042.25cm2
2nd Method : Let O be the centre.
From O draw OD BC
BC
From O draw OD
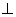 BC
BC 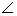 AOC =
AOC = 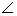 BOC =
BOC = 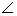 COA =
COA =  =
= 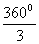 = 1200
= 1200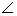 BOD =
BOD = 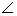 COD =600 ………[From(i)]
COD =600 ………[From(i)]Now,inrt .
 ODA,cos60 =
ODA,cos60 =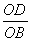
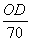
In rt. ODB,sin 600 = BD/OB
ODB,sin 600 = BD/OB
 ODB,sin 600 = BD/OB
ODB,sin 600 = BD/OB√3/2 = BD/70
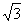
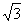 cm
cm BC=2BD=2(35
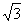 )=70
)=70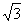
Total area of the design= a rod circle–ar of
 ABC
ABC= 22 x/7 (70)2 -
=22x / 7 (70)2 - √3/4(70 √3 )2
………..
=(70)2 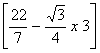
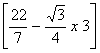
=4900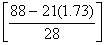
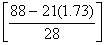
= 175(88–36.33)
=175 X 51.67=9042.25 cm2 )
Or
Calculate the area other than the area common between two quadrants of circles of radius 16 cm each, which is shown as the shaded region in Fig. 6.
=2[(16)2 -22/7 x 64]
=2 [256 – 1408/7] = 2 (256 – 201.4)
=2(54.86)=109.72cm2
SECTION D
Questions number 26 to 30 carry 6 marks each.
Q. 26 A motorboat whose speed in still water is 5 km/h, takes 1 hour more to go 12 km upstream
than to return downstream to the same spot. Find the speed of the stream.
than to return downstream to the same spot. Find the speed of the stream.
Sol. Let the speed of the stream = x km/hr
Then the speed of motorboat upstream = (5 – x) km/hr
and the speed of motorboat downstream = (5 + x) km/hr
Distance = 12 km
According to the question,
Then the speed of motorboat upstream = (5 – x) km/hr
and the speed of motorboat downstream = (5 + x) km/hr
Distance = 12 km
According to the question,
But speed can not be –ve
Q. 27. A man on the deck of a ship 14 m above water level, observes that the angle of elevation ofthe top of a cliff is 60° and the angle of depression of the base of the cliff is 30°. Calculate the distance of the cliff from the ship and the height of the cliff. [Take 3 = 1.732]
Sol. Let AB be the deck of a ship and CE be the cliff.Or
The angles of depression of the top and the bottom of a 9 m high buildling from the top of a tower are 30° and 60° respectively. Find the height of the tower and the distance between the building and the tower.
Sol. Let AC be the towerand DE be the building.
Let AC = y m
and DC = EB = x m
Q. 28. Prove that, in a triangle, if the square on one side is equal to the sum of squares of the other two sides, then the angle opposite to the first side is a right angle. Using the above, show that in an isosceles triangle ABC with AC = BC, if AB2 = 2AC2 then ABC is a right triangle.
Sol. Part I : See Theorem 4,
Page (xxxii).
Part II : AB2 = 2AC2
…(Given)
AB2 = AC2 + AC2
AB2 = AC2 + BC2
…[AC = BC (given)]
Or
Prove that the lengths of tangents drawn from an external point to a circle are equal. Use the above result in the following :A circle is inscribed in a ΔABC, touching AB, BC and AC at P, Q and R
respectively, as shown in
respectively, as shown in
Fig. 7. If AB = 10 cm,
AR = 7 cm and RC = 5
cm, then find the length of BC.
AR = 7 cm and RC = 5
cm, then find the length of BC.
Sol.
Part I : See Theorem 6, Page (xxxii).
Part II : AP = AR = 7 cm …(Given theorem)
QC = RC = 5 cm …(Given theorem)
BP = AB – AP
= 10 – 7 = 3 cm
BQ = BP = 3 cm …(Given theorem)
 BC = BQ + QC = 3 + 5 = 8 cm
BC = BQ + QC = 3 + 5 = 8 cm
Q. 29. A bucket made up of a metal sheet is in the form of a frustum of a cone. The depth of the bucket is 24 cm and the diameters of the top and the bottom are 30 cm and 10 cm respectively. Find the cost of milk which can completely fill the bucket at the rate of Rs. 25 per litre.QC = RC = 5 cm …(Given theorem)
BP = AB – AP
= 10 – 7 = 3 cm
BQ = BP = 3 cm …(Given theorem)
Q. 30. The following table gives production yield per hectare of wheat of 100 farms of a village :
| Production yield (kg/hectare) | Number of farms |
| 40 -45 | 4 |
| 45 -45 | 6 |
| 50 -55 | 16 |
| 55-60 | 20 |
| 60 -65 | 30 |
| 65 -70 | 24 |
Change the distribution to a ‘more than type’distribution, and draw its ogive.
Sol.
| Production yield (kg/hectare) | Number of farms | Production more than | c.f. |
| 40 -45 | 4 | 40 | 100 |
| 45 -50 | 6 | 45 | 96 |
| 50 -55 | 16 | 50 | 90 |
| 55 -60 | 20 | 55 | 74 |
| 60 -65 | 30 | 60 | 54 |
| 65 -70 | 24 | 65 | 24 |
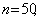






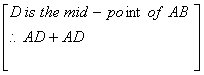









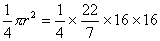













No comments:
Post a Comment